Tutorial 1 - Analyzing scRNA-seq data at the Protein Activity Level
This Tutorial will guide the user thorugh the analysis of single-cell RNA-seq (scRNA-seq) data at the Protein Activity level using pyviper. Specifically, we will show how to transform a gene expression signature generated from sparse scRNA-seq data into a protein activity matrix using the VIPER algorithm. After a brief description of the installation procedure and the modules needed, this Jupyter Notebook is organized in the following sections.
Table of Contents
Install PyVIPER
Install pyviper from PyPI using pip. Alternatively, refer to the README in the current GitHub to install from the local directory.
[1]:
# !pip install viper-in-python
Import modules
Load pyviper and additional modules required used in this tutorial.
[2]:
import pyviper
import scanpy as sc
import anndata
import pandas as pd
import numpy as np
import random
import warnings
warnings.filterwarnings("ignore", message=".*The 'nopython' keyword.*") # for jit decorator issue with sc.pp.neighbors (09/30/2023)
Setup the path to the data.
[3]:
data_location = "https://zenodo.org/records/10059791/files/"
We will import the data directly from the above link. Optionally, users are allowed to download the files from here and to load them from their local computer. If the second option is preferred, the following lines can be uncommented and run to download the data on Unix systems and set the working directory to the path where the data will be stored.
[4]:
#!mkdir Tutorial_1_data_dir
#%cd Tutorial_1_data_dir
#!curl -O https://zenodo.org/records/10059791/files/Tutorial_1_gExpr_fibroblast_5802.tsv.gz -O https://zenodo.org/records/10059791/files/fibroblast-net.tsv
#data_location = !pwd
#data_location = data_location[0]+"/" # new value for data if working on data downloaded locally
Step 1. Load a gene expression signature for single-cells
Load a gene expression signature to be used as input for the viper function for Protein Activity inference and store it as an AnnData object to enable interoperability with scanpy. The time required for this process is approximately 5 s and 30 s if loading from the local directory or remote url, respectively.
[5]:
gene_expr_path = data_location + "Tutorial_1_gExpr_fibroblast_5802.tsv.gz"
gene_expr_signature = pd.read_csv(gene_expr_path, sep="\t") # read from remote
gene_expr_signature = sc.AnnData(gene_expr_signature) # convert to AnnData object
This signature was generated from a population of cancer-asssociated fibroblasts (CAFs) from publicly avaiable data from Peng et al., 2019 following a similar procedure to the one described in Tutorial 2.
Display matrix dimensions with cells on rows and features (genes) on columns.
[6]:
gene_expr_signature
[6]:
AnnData object with n_obs × n_vars = 5802 × 5000
Step 2. Load an inspect a lineage-specific gene regulatory network
Load and inspect a lineage-specific gene regulatory network generated with the ARACNe3. The time required to load a network is approximately 1 s (from local directory) and 40 s (from remote url).
[7]:
network_path = data_location + "fibroblast-net.tsv" # path to ARACNe network
network = pd.read_csv(network_path, delimiter="\t")
Convert the pd.DataFrame to an object of class Interactome to enable easier manipulation. Show the number of regulons using the size() method. You can see all available methods by typing help(pyviper.Interactome).
[8]:
network_interactome = pyviper.Interactome('fibroblasts', network) # convert to class Interactome
network_interactome.size() # show number of regulons in the Interactome
[8]:
6437
Display the first 5 interactions in the regulatory network. mor and likelihood are the mode of regulation of the given regulator-target pair and the likelihood of the interaction, respectively. Algorithms other than ARACNe can be used to generate gene regulatory networks, but we recommend postprocessing the output to suitable data formats to use viper.
[9]:
network_interactome.net_table.head()
[9]:
| regulator | target | mor | likelihood | |
|---|---|---|---|---|
| 0 | AATF | CCM2 | 0.012159 | 0.999799 |
| 1 | AATF | THOC2 | 0.007487 | 0.999597 |
| 2 | AATF | RAP1A | -0.021062 | 0.999396 |
| 3 | AATF | SFT2D1 | 0.019400 | 0.999195 |
| 4 | AATF | DNAJC2 | 0.047129 | 0.998993 |
Filter out targets in the Interactome that are not present in the gene expression matrix. This step is recommended before running viper.
[10]:
network_interactome.filter_targets(gene_expr_signature.var_names)
Removed 3047484 targets.
As an example, display the number of targets of two regulators, MYC and EGFR2.
[11]:
n_MYC = len(network_interactome.get_reg('MYC')) # number of MYC targets in the network
n_EGFR = len(network_interactome.get_reg('EGFR')) # number of SERPINA12 targets in the network
print("The number of targets of MYC and SERPINA12 are " + str(n_MYC) + " and " + str(n_EGFR) + ", respectively.")
The number of targets of MYC and SERPINA12 are 284 and 183, respectively.
Step 3. Convert the gene expression signature into a protein activity matrix using VIPER
viper transforms a gene expression signature into a protein activity matrix by performing enrichment analysis on regulons. Two methods for enrichment analysis are available, aREA (default) and NaRnEA (by setting enrichment="narnea").
Method 1 - protein activity inference using aREA
As shown above, different regulators can have a different number of targets. Prune each regulon to have the same number of targets (50 in this case). This preprocessing step is advisable to avoid regulators with exceedingly number of targets dominating those having fewer in the computation of Normalized Enrichment Scores (NES), to make NES comparable.
[12]:
network_pruned = network_interactome.copy() # generate a copy of the unpruned network before pruning it
network_pruned.prune(max_targets=50,eliminate=True) # prune interactome to have exactly 50 targets
Removed 664967 targets.
Removed 47 regulators.
Now all the regulators in the network have exactly 50 transcriptional targets. See e.g. MYC and EGFR2.
[13]:
n_MYC = len(network_pruned.get_reg('MYC')) # number of MYC targets in the network
EGFR = len(network_pruned.get_reg('EGFR')) # number of SERPINA12 targets in the network
print("Number of MYC targets: " + str(n_MYC) + "\nNumber of EGFR targets: " + str(EGFR))
Number of MYC targets: 50
Number of EGFR targets: 50
Run viper to compute the protein activity matrix with aREA.
Mandatory inputs to viper are 1. a gene expression signature and 2. a gene regulatory network. Set the viper output to be an ndarray (The default output would be an AnnData object). The expected runtime is approximately 10-15 s.
[14]:
ProtAct_aREA = pyviper.viper(gex_data=gene_expr_signature, # gene expression signature
interactome=network_pruned, # gene regulatory network
enrichment = "area",
output_as_anndata=False,
njobs=1,
verbose=False)
ProtAct_aREA contains the activity of every regulatory protein described by its NES for each single cell.
[15]:
ProtAct_aREA # display the protein activity matrix
[15]:
| AAMP | AATF | ABCA1 | ABCA12 | ABCA3 | ABCA7 | ABCA8 | ABCB1 | ABCB4 | ABCB5 | ... | ZSWIM5 | ZSWIM6 | ZSWIM7 | ZWINT | ZXDA | ZXDB | ZXDC | ZYX | ZZEF1 | ZZZ3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1_AAACCTGAGATGTCGG | -4.958661 | -6.340532 | 5.591431 | 0.026641 | -0.952873 | 0.024560 | 6.763799 | -0.220392 | -0.051190 | 0.051432 | ... | -0.079490 | -0.701844 | -6.250761 | -0.011008 | -1.692154 | 0.018511 | -0.282504 | -5.392813 | 0.063155 | -0.051505 |
| T1_AACTGGTTCTAACGGT | -7.377609 | -6.798952 | -6.550723 | 1.626537 | 0.039575 | 0.132152 | -9.076912 | 0.024765 | -0.054462 | 0.046818 | ... | -0.039977 | -1.666785 | -5.924595 | -0.070319 | 1.271308 | -0.008729 | 0.347169 | 8.320215 | -0.504002 | 0.030807 |
| T1_AAGGTTCGTGTCAATC | -6.881051 | -6.227523 | -5.938090 | 0.248098 | -0.075314 | 0.431982 | 8.251861 | 0.353197 | -0.024522 | 0.019459 | ... | -0.217323 | 1.762852 | -5.514518 | -0.042265 | 0.096729 | -0.072773 | -0.204381 | -8.505392 | 0.020706 | -0.005608 |
| T1_ACAGCCGTCAAGCCTA | -7.370794 | -5.838071 | -5.957978 | -0.356005 | -0.611744 | 0.173595 | 9.672680 | 1.063066 | 0.021172 | 0.004548 | ... | -0.023732 | -1.628548 | -5.588137 | 0.008851 | -0.634454 | -0.010447 | -0.095425 | -7.882212 | 0.052736 | -0.012834 |
| T1_AGACGTTAGGCGACAT | -7.160952 | -6.351434 | -6.644756 | -0.020971 | 0.197701 | 0.093815 | -7.264978 | 0.045201 | -0.019334 | -0.005189 | ... | 0.016033 | -1.136795 | -6.277997 | 0.015763 | 1.310698 | 0.022143 | -1.424293 | -7.538373 | -0.124011 | -0.004775 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| T24_TTGCGTCCAGACAAAT | -3.853770 | -3.744690 | -5.746431 | -0.770776 | -0.006618 | 0.075021 | 4.486073 | 0.032965 | -0.072500 | 0.025214 | ... | -0.040233 | 2.667354 | 5.823175 | 0.706549 | -0.558190 | -0.006004 | 0.520060 | 4.892258 | 0.977937 | 0.303938 |
| T24_TTGCGTCCATTAACCG | -7.183422 | 6.414101 | -6.321449 | -1.070418 | -0.604463 | 0.162847 | -9.382614 | 0.062170 | -0.088907 | -0.006882 | ... | -0.078167 | -1.471368 | -6.268302 | -0.468904 | -1.011935 | 0.028369 | 0.770259 | 7.526919 | 0.083573 | 0.024982 |
| T24_TTTATGCTCCTTTACA | -7.402969 | -6.773775 | -6.956773 | 0.873204 | 0.104889 | -0.613706 | 8.306039 | -0.014412 | -0.003422 | -0.008079 | ... | -0.045534 | -2.281823 | 6.220555 | -0.622250 | 0.353278 | -0.006841 | -0.106645 | -7.967557 | 0.531523 | -0.018268 |
| T24_TTTCCTCCACCGGAAA | -5.338859 | -5.148087 | -4.857930 | -0.589181 | 1.378187 | 0.016195 | -6.906513 | -0.113458 | -0.017487 | -0.001037 | ... | -0.038365 | -1.267985 | 5.216135 | -0.087870 | -0.819144 | -0.005551 | -0.701608 | -4.798419 | 0.062763 | -0.084813 |
| T24_TTTGCGCTCCTTTCGG | 6.571542 | -5.770066 | -6.173451 | 1.207757 | -0.328110 | 0.027743 | 7.764931 | 0.028870 | -0.032131 | 0.034307 | ... | -0.153165 | -2.324143 | -4.856275 | 0.808057 | -0.381149 | 0.053897 | -0.455522 | -6.480079 | 0.033859 | -0.373861 |
5802 rows × 6390 columns
Method 2 - protein activity inference using (matrix)-NaRnEA
Run viper to compute the protein activity matrix using (matrix-based) NaRnEA .
Compute the protein activity using viper with NaRnEA as the enrichment method. Unlike aREA, the NaRnEA framework is suitable also for regulons of different size. Store the output in an AnnData object (default).
[16]:
ProtAct_NaRnEA = pyviper.viper(gex_data=gene_expr_signature, # gene expression signature
interactome=network_interactome, # gene regulatory network
enrichment = "narnea",
eset_filter=False,
njobs=1,
verbose=False)
Show the output type and length of ProtAct_NaRnEA.
[17]:
ProtAct_NaRnEA # display the protein activity matrix as AnnData object
[17]:
AnnData object with n_obs × n_vars = 5802 × 6413
uns: 'gex_data'
layers: 'pes'
When run with the NaRnEA method, viper returns an additional layer, pes that stores the Proportional Enrichment Score (PES) of each regulator, a measure of protein activity in the \(-1 \le PES \le 1\) interval that can be used as an enhanced measure of effect size of each regulon’s activity. For further details, see Griffin et al., 2022.
Display NES protein activity matrix.
[18]:
ProtAct_NaRnEA.to_df() # NES matrix
[18]:
| AAMP | AATF | ABCA1 | ABCA12 | ABCA3 | ABCA7 | ABCA8 | ABCB1 | ABCB4 | ABCB5 | ... | ZSWIM5 | ZSWIM6 | ZSWIM7 | ZWINT | ZXDA | ZXDB | ZXDC | ZYX | ZZEF1 | ZZZ3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1_AAACCTGAGATGTCGG | 4.721734 | -6.619827 | 7.008813 | 1.861781 | 1.856598 | -0.870238 | 14.555466 | -0.624870 | -0.835634 | 0.415443 | ... | -1.877274 | 3.158300 | -7.010895 | -0.767114 | -2.016624 | 1.473462 | 2.726915 | 5.796276 | 2.409854 | -2.594848 |
| T1_AACTGGTTCTAACGGT | -7.194335 | 7.539468 | 9.435460 | 4.098622 | -0.469555 | 1.067867 | -18.895628 | 1.415011 | -0.808934 | 1.093563 | ... | 2.213714 | -3.225383 | -7.223655 | 0.832463 | 1.240214 | -1.571365 | -1.406364 | 12.754583 | 1.835522 | 2.965396 |
| T1_AAGGTTCGTGTCAATC | 8.892053 | -9.453808 | -10.276663 | 3.200662 | -1.276665 | 0.668082 | 20.592220 | 0.475050 | -0.928214 | 0.497169 | ... | 1.669964 | 3.418652 | -8.993046 | -1.793087 | -0.958978 | -2.596414 | 1.049315 | -11.111879 | -1.967781 | -2.485891 |
| T1_ACAGCCGTCAAGCCTA | 7.851400 | 6.905695 | 9.582031 | -2.862549 | -0.883946 | -1.470669 | 23.073534 | -0.614457 | 1.140870 | 0.949438 | ... | -1.179793 | -2.539163 | -6.815755 | -1.127239 | -1.584070 | 1.258887 | 2.088022 | -11.702254 | 2.173031 | 2.511354 |
| T1_AGACGTTAGGCGACAT | 7.647149 | 6.960122 | -8.842428 | 2.599533 | 0.562035 | -0.706634 | -15.241218 | 0.168039 | 2.954947 | -0.942813 | ... | 1.897963 | -2.463266 | -9.299325 | 0.864452 | 2.009431 | -1.286205 | -2.902146 | 8.258941 | -2.184118 | 3.036592 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| T24_TTGCGTCCAGACAAAT | 3.936121 | 3.912197 | -7.635411 | -2.268020 | 0.557243 | -1.325284 | 10.868199 | 0.819879 | -1.106013 | 1.725982 | ... | -2.446716 | 2.681818 | 5.761685 | 0.989011 | -2.355896 | -0.963434 | 1.598874 | 6.739289 | 2.979156 | 1.230419 |
| T24_TTGCGTCCATTAACCG | -7.200858 | 7.800428 | 8.200803 | -2.343332 | -1.674645 | 1.416084 | -19.099210 | 0.633930 | -0.581409 | -1.299787 | ... | 1.167182 | -2.944020 | 7.269258 | -0.951725 | -1.750199 | 1.705520 | -1.838097 | 10.667582 | 1.591999 | 2.984735 |
| T24_TTTATGCTCCTTTACA | -7.106027 | 8.048133 | -8.375441 | 2.619907 | 0.908485 | -2.109688 | 20.656478 | -0.355086 | 0.885489 | -0.590344 | ... | 1.123289 | 2.807651 | 6.441253 | 1.058726 | 1.446795 | -1.593226 | 1.463587 | -10.230168 | 1.784666 | 2.937815 |
| T24_TTTCCTCCACCGGAAA | -6.272371 | -5.982345 | -6.917609 | -3.526581 | 0.889230 | -1.033967 | -11.206110 | 0.544282 | -1.331863 | 0.820132 | ... | 1.272478 | -3.339912 | 5.365629 | -2.224107 | -1.598793 | -1.075789 | 0.956203 | -6.464254 | -1.202947 | 2.896665 |
| T24_TTTGCGCTCCTTTCGG | 7.662765 | 5.670811 | -7.459790 | 3.314262 | 1.253227 | -2.886863 | 15.754894 | 0.312123 | -1.264925 | 1.451191 | ... | -1.528563 | -2.797515 | 5.459777 | 1.624329 | 1.406323 | 1.839792 | 1.615043 | -6.028920 | 1.614101 | 2.219795 |
5802 rows × 6413 columns
Display the PES protein activity matrix.
[19]:
ProtAct_NaRnEA.to_df(layer="pes") # PES matrix
[19]:
| AAMP | AATF | ABCA1 | ABCA12 | ABCA3 | ABCA7 | ABCA8 | ABCB1 | ABCB4 | ABCB5 | ... | ZSWIM5 | ZSWIM6 | ZSWIM7 | ZWINT | ZXDA | ZXDB | ZXDC | ZYX | ZZEF1 | ZZZ3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1_AAACCTGAGATGTCGG | 0.241036 | -0.304539 | 0.281272 | 0.075302 | 0.065838 | -0.030641 | 0.378996 | -0.021552 | -0.028560 | 0.013191 | ... | -0.058449 | 0.109650 | -0.352310 | -0.026813 | -0.070147 | 0.050491 | 0.092683 | 0.262461 | 0.085498 | -0.092541 |
| T1_AACTGGTTCTAACGGT | -0.377690 | 0.314298 | 0.353704 | 0.161168 | -0.015489 | 0.036149 | -0.498108 | 0.047821 | -0.026871 | 0.033680 | ... | 0.065591 | -0.115920 | -0.365330 | 0.029592 | 0.042860 | -0.053004 | -0.044979 | 0.546406 | 0.062974 | 0.098528 |
| T1_AAGGTTCGTGTCAATC | 0.411896 | -0.426499 | -0.463221 | 0.121913 | -0.040238 | 0.021839 | 0.489513 | 0.015586 | -0.029855 | 0.014794 | ... | 0.047508 | 0.107629 | -0.455912 | -0.057534 | -0.030965 | -0.085069 | 0.034159 | -0.548071 | -0.067285 | -0.085520 |
| T1_ACAGCCGTCAAGCCTA | 0.374073 | 0.280960 | 0.347664 | -0.111102 | -0.028572 | -0.049797 | 0.563166 | -0.020199 | 0.037355 | 0.028794 | ... | -0.035533 | -0.090658 | -0.345054 | -0.037077 | -0.052268 | 0.041115 | 0.068854 | -0.577137 | 0.073317 | 0.081781 |
| T1_AGACGTTAGGCGACAT | 0.367849 | 0.286135 | -0.395323 | 0.101320 | 0.019492 | -0.024048 | -0.399215 | 0.005632 | 0.097293 | -0.028792 | ... | 0.055635 | -0.088110 | -0.469940 | 0.030555 | 0.068925 | -0.043036 | -0.091780 | 0.348528 | -0.076160 | 0.099715 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| T24_TTGCGTCCAGACAAAT | 0.204764 | 0.174948 | -0.337461 | -0.093431 | 0.019970 | -0.047278 | 0.288253 | 0.028819 | -0.038329 | 0.055596 | ... | -0.077137 | 0.094923 | 0.273529 | 0.036050 | -0.083271 | -0.033768 | 0.054981 | 0.311843 | 0.107347 | 0.043343 |
| T24_TTGCGTCCATTAACCG | -0.380139 | 0.335792 | 0.321417 | -0.094081 | -0.056706 | 0.048863 | -0.508320 | 0.021759 | -0.019652 | -0.040733 | ... | 0.035385 | -0.106378 | 0.330039 | -0.032770 | -0.060073 | 0.057730 | -0.060230 | 0.473601 | 0.055765 | 0.101769 |
| T24_TTTATGCTCCTTTACA | -0.374351 | 0.343964 | -0.370559 | 0.104330 | 0.031898 | -0.073233 | 0.525972 | -0.012040 | 0.029794 | -0.018420 | ... | 0.033870 | 0.095181 | 0.289916 | 0.037852 | 0.050491 | -0.054353 | 0.049172 | -0.502406 | 0.062200 | 0.099569 |
| T24_TTTCCTCCACCGGAAA | -0.333195 | -0.276134 | -0.311172 | -0.141074 | 0.031418 | -0.035984 | -0.299382 | 0.018663 | -0.044897 | 0.025645 | ... | 0.038321 | -0.121415 | 0.238997 | -0.075915 | -0.054567 | -0.036805 | 0.032295 | -0.321070 | -0.042854 | 0.097915 |
| T24_TTTGCGCTCCTTTCGG | 0.387580 | 0.246106 | -0.329504 | 0.133253 | 0.044279 | -0.101097 | 0.406666 | 0.010766 | -0.042976 | 0.045788 | ... | -0.047366 | -0.101365 | 0.250277 | 0.058417 | 0.049472 | 0.062629 | 0.054655 | -0.296234 | 0.056873 | 0.076209 |
5802 rows × 6413 columns
Notice that when setting the viper output to be an object of class AnnData, the input gene expression matrix is saved under the attribute gex_data of the output AnnData object:
[20]:
ProtAct_NaRnEA.uns["gex_data"][0:5,0:5].to_df()
[20]:
| RP11-54O7.3 | SAMD11 | PLEKHN1 | RP11-54O7.17 | HES4 | |
|---|---|---|---|---|---|
| T1_AAACCTGAGATGTCGG | -0.145409 | -0.513375 | -0.130302 | -0.134275 | 1.855504 |
| T1_AACTGGTTCTAACGGT | -0.108846 | -0.390002 | -0.096722 | -0.101255 | 2.064095 |
| T1_AAGGTTCGTGTCAATC | -0.084144 | -0.306366 | -0.074026 | -0.078937 | 1.387576 |
| T1_ACAGCCGTCAAGCCTA | -0.099796 | -0.359357 | -0.088408 | -0.093080 | -0.622520 |
| T1_AGACGTTAGGCGACAT | -0.099830 | -0.359472 | -0.088440 | -0.093111 | 3.986061 |
Step 4. Analyze single-cells at the Protein Activity level
This section presents some useful postprocessing functions that can be used on the protein activity matrix.
First, set the set of regulatory proteins to be those for the human species. This is step is redundant, since pyviper sets "human" as default, but it demonstrates how to have complete control over the analysis, if fine-tuning is desired.
[21]:
pyviper.config.set_regulators_species_to_use(species="human")
Run PCA to reduce the dimensionality of the dataset, by projecting the PES of transcriptional regulators (TFs) and co-transcriptional regulators (coTFs) by setting filter_by_feature_groups=["tfs", "cotfs"]. In this example, we focus on TFs and coTFs, major mechanistic determinants of cell state as shown in Paull et al., 2021 and Califano & Alvarez, 2016.
Possible options for this parameter are ["tfs", "cotfs", "sig", "surf"], where the latter refer to signaling proteins and surface markers, respectively. The default (None) uses all the features in the protein activity matrix.
[22]:
random.seed(0)
pyviper.tl.pca(ProtAct_NaRnEA, layer="pes", filter_by_feature_groups=["tfs","cotfs"], zero_center=True, svd_solver='arpack', random_state=0)
The tl module provides wrappers to several scanpy.tl functions, and it can be used to simplify the postprocessing of protein activity data, for instance by subsetting the class of regulatory proteins to analyze, as shown in the cell above.
Compute the neighbors graph of cells using the PCA representation of the protein activity matrix. For sake of simplicity, set n_neighbors = 20and n_pcs = 50 (please, notice that typically, these parameters need tuning).
[23]:
sc.pp.neighbors(ProtAct_NaRnEA, metric="correlation", n_neighbors=20, n_pcs=50, random_state=0)
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
Cluster cells based on their protein activity profiles using the Leiden algorithm with resolution=0.1 (in real-world applications this parameter should also be optimized).
[24]:
sc.tl.leiden(ProtAct_NaRnEA, resolution=0.1, n_iterations=-1, random_state=0)
Generate a UMAP embedding for the graph.
[25]:
sc.tl.umap(ProtAct_NaRnEA, random_state=0)
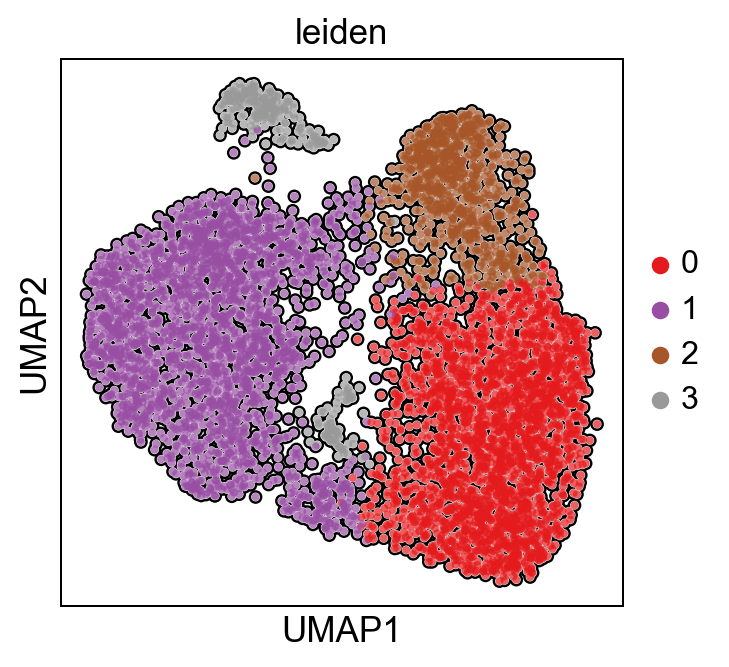
Display the 2-dimensional UMAP embedding using the pyviper.pl module for easier post-processing of key protein activity features. Color by cluster.
[26]:
sc.set_figure_params(dpi=90)
n_cells = ProtAct_NaRnEA.shape[0]
dot_size = 120000 / n_cells*2
pyviper.pl.umap(ProtAct_NaRnEA, color='leiden', palette="Set1", size=dot_size,add_outline=True)
/Users/lucazanella7/mambaforge/lib/python3.10/site-packages/scanpy/plotting/_tools/scatterplots.py:369: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
ax.scatter(
/Users/lucazanella7/mambaforge/lib/python3.10/site-packages/scanpy/plotting/_tools/scatterplots.py:379: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
ax.scatter(
/Users/lucazanella7/mambaforge/lib/python3.10/site-packages/scanpy/plotting/_tools/scatterplots.py:392: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
cax = scatter(
Identify the most active regulators in each cluster by cluster-based integration of their NES using the Stouffer’s method:
where \(NES^C_j\) denotes the integrated NES for regulator \(j\) in cluster \(C\), \(NES_{k,j}\) is the NES of regulator \(j\) in cluster \(C\) and \(n^C\) is the number of cells in cluster \(C\).
[27]:
NES_integrated = pyviper.pp.stouffer(ProtAct_NaRnEA, "leiden", filter_by_feature_groups=["tfs","cotfs"], compute_pvals=False, return_as_df=True) # Stouffer integration
NES_integrated
[27]:
| AATF | ABCG1 | ABCG4 | ABLIM3 | ABT1 | ACAD8 | ACTN2 | ACTR5 | ADH1A | ADNP | ... | ZSWIM1 | ZSWIM3 | ZSWIM4 | ZSWIM5 | ZSWIM6 | ZSWIM7 | ZXDA | ZXDB | ZXDC | ZZEF1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0_scores | 67.525573 | 115.613861 | 27.080476 | -28.436313 | -132.404139 | -33.429712 | -13.909552 | -47.931126 | 4.051971 | -29.487164 | ... | -11.106391 | -22.387029 | 62.365929 | 20.721141 | -66.658539 | -30.107811 | -11.112864 | 1.628075 | -26.403334 | -22.699427 |
| 1_scores | -91.800207 | -142.827803 | -17.348848 | -18.037332 | 25.121737 | 36.583034 | -0.532866 | -34.507518 | 11.575850 | -161.079785 | ... | 30.393149 | 26.228487 | -35.711558 | 10.563270 | -54.133110 | 71.437503 | 22.445477 | -9.705253 | 22.332898 | 26.533621 |
| 2_scores | 155.866707 | 112.772956 | -28.882646 | -12.207053 | 269.112806 | 34.378121 | -17.958921 | -0.020872 | 11.181962 | -156.887473 | ... | 20.037990 | -30.555842 | -4.616144 | -4.629360 | -77.501573 | 52.334168 | 3.893929 | -28.350717 | 23.055552 | -45.316784 |
| 3_scores | 60.353173 | -7.015611 | -18.430420 | -13.188699 | 45.879802 | 13.423553 | -6.909312 | -5.033798 | 4.884707 | -35.414756 | ... | 14.532806 | -0.763232 | 6.192970 | 5.708014 | -6.913988 | 41.258296 | 15.351770 | -15.435729 | 22.549805 | -13.521504 |
4 rows × 2164 columns
Analogously, the stouffer function can be employed to produce an output directly on the AnnData object. Remove ribosomal proteins from the Stouffer-integrated matrix (ribosomal protein genes are among the most highly expressed genes in most cell types).
[28]:
filtered_proteins = NES_integrated.columns[~NES_integrated.columns.str.startswith('RP')].to_list() # Exclude columns starting with 'RP' from integrated matrix
NES_integrated = NES_integrated.loc[:,filtered_proteins] # remove ribosomal proteins from DataFrame
Select the 10 most activated regulatory protein in each cluster.
[29]:
active_proteins = NES_integrated.apply(lambda row: row.nlargest(10).index.tolist(), axis=1) # the top 10 most activated proteins in each cell type
active_proteins
[29]:
0_scores [INHBA, MMP14, ID3, LOXL2, HOPX, RUNX2, LEF1, ...
1_scores [TSHZ2, NFIA, NFIB, ZBTB16, TCF21, NR2F1, ZFP3...
2_scores [ENO1, NACA, PFDN5, LOXL2, BTF3, HMGA1, CCDC85...
3_scores [FOSB, NR4A1, ELL2, ID4, REL, JUND, NR4A2, NR4...
dtype: object
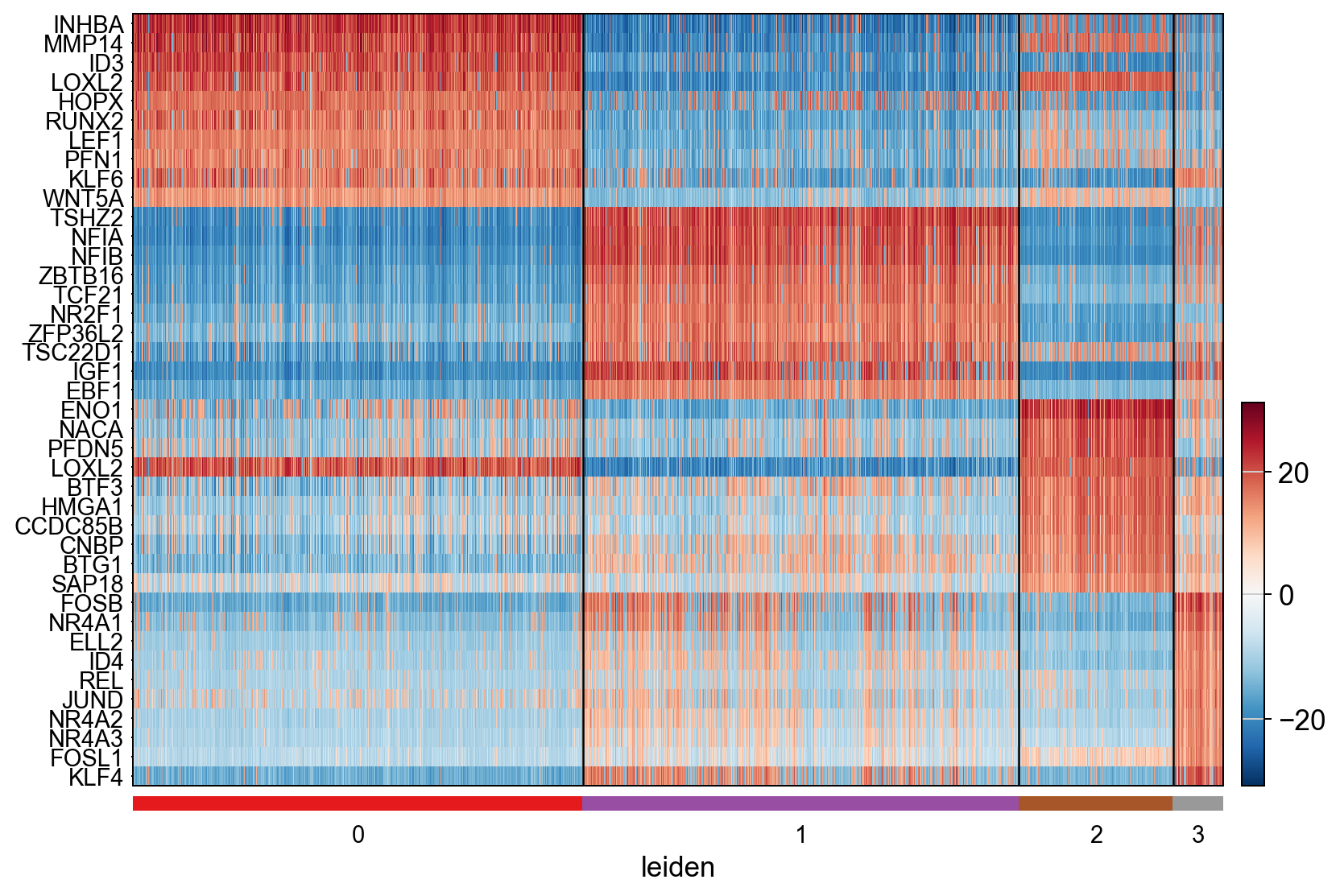
Finally, display the top activated proteins from ProtAct_NaRnEA on a heatmap
[30]:
protein_set = active_proteins.sum() # protein set to display on the heatmap
ax = pyviper.pl.heatmap(ProtAct_NaRnEA, var_names=protein_set, groupby="leiden", vcenter=0, cmap="RdBu_r",dendrogram=False,swap_axes=True, show_gene_labels=True)
Key takeaways
This Tutorial describes how to inspect and process gene regulatory networks, by manipulating objects of class Interactome, and shows how to generate protein activity profiles from single-cell data using the viper function. Last, we presented key functions for the post-processing and visualization of protein activity data. In Tutorial 2 we will introduce the user to the generation of suitable gene expression signatures for viper and extend the VIPER analysis to simultaneously account
for multiple cell pupulations through the exploitation of the metaVIPER paradigm.